원문 링크 : 넷츠고 프로머동의 금승철님이 강좌글을 보기 편하게 편집한 것이며, 원문이 없어져서 링크는 걸지 못함.
기본적인 알고리즘 강좌
제홈페이지는 http://myhome.netsgo.com/jetsong,
Email은 jetsong@netsgo.com입니다.
프로그램을 작성하는데 있어 ‘일의 처리 방법’이라는 것은 ‘알고리즘’에 해당한다고 할수 있다. 같은 일을 처리하는 방법도 여러 가지가 있을 수 있듯이 하나의 문제를 풀기 위한 알고리즘도 여러 가지일 수 있다. 그리고, 또한 처리 방법에 따라서 처리 시간이 달라지듯이 알고리즘에 따라서 수행 시간이 달라진다.
따라서 보다 빠르게 수행되는 프로그램을 원한다면 보다 적당한 알고리즘을 사용해야 하는 것은 당연한 얘기일 것이다.
알고리즘의 구체적인 예들은 너무나 많고, 분야도 방대하기 때문에 여기에 모든 예를 설명할 수는 없다. 따라서, 여기에서는 프로그램을 시작하는 여러분을 위해서 어느 프로그램에서나 거의 공통적으로 필요로 하고 많이 사용되는 알고리즘과 여러분의 흥미를 끌 수 있는 알고리즘 몇 가지만을 소개하고자 한다.
- 1. 탐색(Searching) 알고리즘
- (1) 순차 탐색-강좌1
- (2) 2진 탐색-강좌2
- (3) 해싱(Hashing)-강좌3
- 2. 정렬(Sorting) 알고리즘
- (1) 단순 정렬법-강좌4
- (2) 선택 정렬법(Selection Sorting)-강좌5
- (3) 삽입 정렬법(Insertion Sorting)-강좌6
- (4) 퀵 정렬법(Quick Sorting)-강좌7
- (5) 힙 정렬법(Heap Sorting)-강좌8
- (6) 합병 정렬법(Merge Sorting)-강좌9
- * 알고리즘의 수행시간 분석
마지막으로 알고리즘의 수행시간 분석에 관한 설명을 추가하였다.
이제 강좌의 처음이다…
사용언어는 C++에 대해서 잘 모르시는 분들을 고려하여 C로 설명하려고 한다.
자! 그럼 강좌1을 시작한다….
1. 탐색(Searching) 알고리즘
만일 여러분이 명함을 차곡차곡 받아서 모아두었다고 하자.
혹은 친구들의 전화번호를 수첩에 적어두었다고 하자.
그런데 어느날 누군가에게 전화를 걸어야 할 일이 생겼다.
여러분은 전화번호를 찾기 위해 명함을 혹은 수첩의 전화번호를 뒤져야 한다.
그러면 어떤 방식으로 원하는 전화번호를 찾아낼 것인가?
(1) 순차 탐색
이 같은 문제를 해결하는 가장 간단한 방법은 역시 ‘순차탐색(Sequential Searching혹은 Linear Searching)’일 것이다.
순차탐색의 원리는 아주 일상적인 것으로 간단히 얘기하자면 앞에서부터 차근차근 하나씩 찾아나가는 것을 얘기한다(그림1 참조).
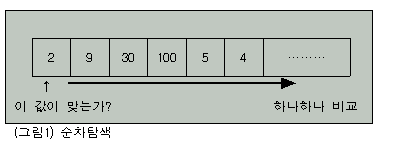
앞에서 얘기한 명함 검색의 예로 살펴봄면 프로그램은 다음과 같이 될 것이다.
while 명함이 남아있음 and 현재 원하는 명함이 아님)
다음 명함
If (명함이 있음)
명함을 반환
else
명함이 없음을 반환
끝
위의 알고리즘을 C언어를 사용하여 하나의 함수로 구현하면 다음과 같은 형식이 된다.
아래의 예에서는 검색의 대상이 되는 자료가 정수형이고,
배열이 a에 저장되어 있으며 NOT-EXIST는 미리 정의된 것으로 가정하였다.
그리고, last-item은 배열의 마지막을 표시하는 정수다.
이후의 검색의 예에서도 이와 같은 가정에 근거한다.
(리스트1) 순차 탐색 알고리즘의 구현 예
{
int curr_item;
curr_item = 0;
While ((curr_item <= last_item) && (a[curr_item] != key))
curr_item++;
if (curr_item <= last_item)
return curr_item;
else
return NOT_EXIST;
}
이와 같은 순차탐색의 수행 속도를 약간 향상시키는 방법으로 ‘보초(sentinel)’를 세우는 방법이 있다.
이 방법을 사용하면 루핑에서 현재 항목이 마지막 항목인지에 대한 검사를 할 필요가 없으므로 검색 속도를 향상시킬 수가 있다.
구체적인 구현 방법은 배열의 마지막 항목의 다음에 찾고자 하는 값을 미리 넣어 둠으로써 원하는 항목이 없는 경우에도 루핑을 빠져 나올 수 있도록 한 것이다.
이와 같이 배열의 마지막을 지키는 값을 ‘보초’라고 부른다(그림2 참조).
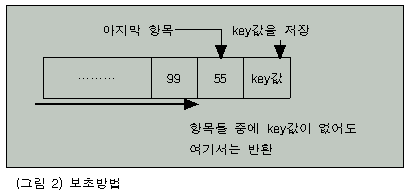
(리스트 2) 보초를 사용하는 개량된 순차 탐색 알고리즘
{
int curr_item;
curr_item = 0;
a[n + 1] = key;
While (a[curr_item] != key)
curr_item++;
if (curr_item <= last_item)
return curr_item;
else
return NOT_EXIST;
}
이와 같이 보초를 사용하는 방법은 다른 많은 경우에 응용될 수 있으므로 기억해 두면 좋다. 단, 이 방법을 사용할 경우에 보초를 위한 메모리를 미리 할당하는 것에 주의하여야 한다.
(2) 2진 탐색
순차 탐색은 가장 이해하기 쉬운 탐색의 방법임에는 틀림없다.
그러나 동시에 가장 느린 탐색 방법임에도 틀림없다.
그러면 보다 빠른 탐색 방법에는 어떤 것이 있을까?
이 얘기를 하기 전에 강좌1에서 얘기한 명함의 경우를 다시 생각해 보자.
명함을 찾을 때에 실제로 앞에서 얘기한 순차탐색의 방법으로 찾는 사람이 있을까?
만일 명함이 ‘가나다’순으로 정리되어 있지 않다면 모르지만 정리 되어 있다면 적당한 위치를 짚어서 살펴 보고, 다시 적당한 위치를 살펴보는 방법을 택할 것이다.
결국 순차적으로 정리되어 있는 자료에 대해서 항상 중간값과 비교해서 어느 쪽에 존재하는가를 판정하는 식의 방법을 사용하는 것을 2진 탐색이라고 한다.
이 방법을 사용하면 자료의 개수가 많아짐에 따라서 순차탐색에 비해 사용되는 시간이 현저하게 절약된다.
이 방법은 앞의 순차 탐색에 비해 다소 복잡해지는 면이 있으나, 그다지 어렵지는 않다.
구현 방법으로는 원하는 값이 존재할 것으로 보이는 영역의 왼쪽 위치와 오른쪽 위치를 중간값과 원하는 값의 비교결과에 따라 변화 시킴으로써 이루어진다(그림3 참조).
아래의 예는 오름차순으로 정리된 자료에 대한 2진 탐색 구현의 예이다.(순차탐색과 같은 가정하에서)
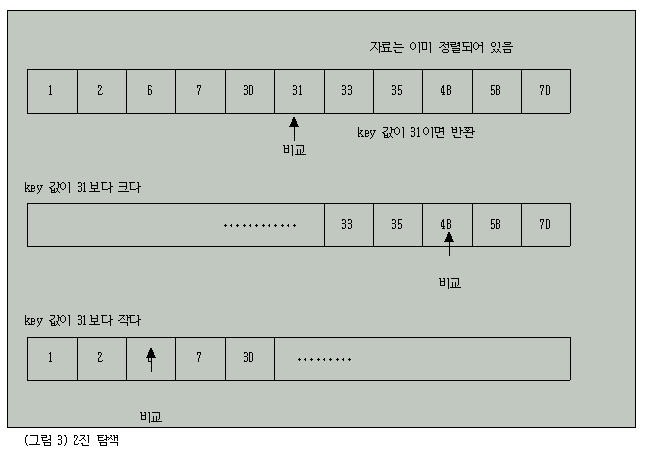
(리스트3) 2진 탐색 알고리즘
{
int left_item, right_item;
int mid_item;
left_item = 0;
right_item = last_item;
while (left_item < right_item)
{
mid_item = (left_item + right_item) / 2;
if (a[mid_item] < key)
left_item = mid_item;
else
right_item = mid_item;
}
if (a[left_item] == key)
return left_item;
else
return NOT_EXIST;
}
위의 예에 대해 간단히 설명을 덧붙이자면, 주어진 while 루핑을 빠져 나오는 경우는 left_item의 값이 right_item 값이나 mid_item의 값과 같아질 경우이다.
따라서, 그 아래에 나오는 if 문에서는 어느 값을 사용하여 비교하여도 상관없지만, mid_item 값을 사용하면 문제가 발생할 수 있다.
즉, last_item이 0이어서 루핑을 거치지 않는 경우에는 mid_item 값이 설정되어 있지 않으므로 주의해야 한다.
(3) 해싱(Hashing)
강좌2에서 얘기한 2진탐색은 상당히 빠르게 원하는 값에 접근하는 방법이다.
그러나, 보다 빠르게 탐색할수 있는 방법이 존재한다.
이 방법은 ‘해싱(Hashing)’ 혹은 ‘분산 기억법(Scatter Storage Technique)’이라고 불리우는데, 실제적으로 가장 빠른 탐색을 제공한다.
앞서의 명함의 예를 다시 한번 생각해 보자. 명함을 보관하는 경우, 대부분의 사람들은 명함첩을 이용한다.
명함첩에는 명함이 시작되는 첫 번째의 자음을 나타내는 표지가 달려있다.
따라서, 우리는 앞서의 2진 탐색을 사용하지 않고도, 찾고자하는 명함이 있는 위치에 상당히 가까이 다가갈 수 있다.
이와 같이 원하는 명함이 있을 위치로 옮겨간 다음에 순차탐색이나 혹은 2진 탐색을 사용하면 앞서의 방법보다 훨씬 빠르게 찾을 수가 있게 된다.
이 방법이 빠른 검색을 제공하는 이유는 단순하다.
즉, 검색할 자료가 보다 잘 정리가 되어 있기 때문이다.
다시 말하면, 데이터의 값에 따라 저장되어야 할 공간이 미리 지정되어 있기 때문이다.
이 방법에서 자료의 값에 따라 저장할 공간을 결정하는 함수를 ‘해싱함수’라고 부르고, 해싱함수를 사용하는 탐색방법을 해싱이라고 한다.
일반적으로 해싱방법은 사용하는 해싱함수에 따라서, 그리고 해싱함수에 의해 같은 값이 나오는(즉, 같은 저장 영역에 존재하는 – 명함의 예에서는 같은 자음으로 시작하는) 자료를 어떻게 보관할 것인가에 따라서 구분될 수가 있다.
해싱을 사용하여 검색하는 구체적인 예를 들어보면, 그림 4와 같이 정수형 자료가 5로 나눈 나머지에 따라서 정리되어 있고, 그 자료가 연결된 리스트(list)의 형태로 저장되어 있다고 하자.
그렇다면 원하는 값에 대한 검색을 위한 루틴은 다음과 같이 구현될 수 있을 것이다.
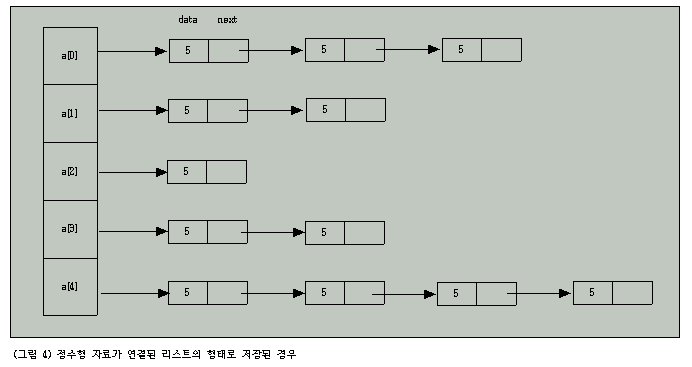
(리스트 4) 해싱과 순차탐색을 같이 사용한 탐색 알고리즘의 예
{
int data;
struct DATALIST *next;
} *DATAPTR;
DATAPTR Hash_Search(int key, DATAPTR *a)
{
DATAPTR b;
b = a[key%5]; // 해싱이 사용된 곳
while (b != NULL)
{
if (key == (b->data))
return b;
b = b->next;
}
return NULL;
}
위의 함수는 앞의 예와는 달리 원하는 값을 검색하지 못했을 경우 NULL값을 반환하게 된다는 것에 주의하기 바란다.
리스트 4의 예에서는 해싱이 사용된 경우는 한번의 해싱으로 검색할 대상을 1/5로 줄여놓았다.
2. 정렬(Sorting) 알고리즘
지금까지 얘기한 탐색과 더불어 일상적으로 가장 많이 사용하는 알고리즘이 바로 자료의 정렬에 관계된 알고리즘이다.
따라서, 여기에 사용되는 알고리즘은 상당히 다양한 편이다.
여기서는 많이 알려진 몇 개만을 소개하기로 하겠다.
(1) 단순 정렬법
자료를 정렬하는 가장 단순한 방법으로는 바로 옆의 데이터와 비교하여 그 결과에 따라서 두 개의 값을 바꾸는 것이다(이 방법을 ‘버블(Bubble) 소트’라고 부른다).
구체적으로 설명하면, 먼저 첫 번째와 두 번째의 값을 비교해서 첫 번째 값이 크면 둘을 바꾼다.
그리고, 두 번째와 세 번째, 세 번째와 네 번째 등등 계속해서 끝까지 비교해 나가면서 바꾼다.
이와 같이 한번 실행하면, 맨끝의 값은 가장 큰 값이 된다.
다시 한번 이와 같은 루프를 돌면 끝에서 2개의 값은 정렬이 된다.
계속해서 이 루프를 자료의 수 만큼(실제로는 자료의 수보다 1이 적은 만큼 – 왜냐하면 자기 자신과 비교한다는 것은 의미가 없기 때문에) 돌게되면 전체의 자료는 정렬되게 된다.
이를 구체적으로 구현된 예로 그림5와 같이 저장된 정수형 자료를 정리하는 함수는 리스트 5와 같이 될 것이다.
(리스트 5) 단순한 정렬(버블, Bubble) 알고리즘
{
int loop1, loop2;
int temp;
for (loop1 = 0; loop1 < last_item; loop1++)
{
for (loop2 = 0; loop2 < (last_item-loop1); loop2++)
{
if (a[loop2] > a[loop2 + 1])
{
temp = a[loop2];
a[loop2] = a[loop2 + 1];
a[loop2 + 1] = temp;
}
}
}
}
(2) 선택 정렬법(Selection Sorting)
강좌 4의 리스트 5의 정렬법을 가만히 관찰해 보면 간단한 방법으로 수행 속도를 향상시킬 수 있는 것을 알 수 있다.
방법을 읽기 전에 잠시만 여러분 스스로 생각을 해보기 바란다.
약간의 힌트를 준다면, 반복해서 수행되는 부분을 주의해서 살펴보라.
리스트 5의 예를 살펴보면, 옆의 값과 비교 후에 바로바로 값을 교환하는 것을 알 수 있다.
이렇게 바로 교환하는 방법은 교환 횟수를 상당히 많게 만든다.
한번의 교환을 하기 위해서는 3번의 치환문이 사용된다.
이것을 다음과 같이 바꾸어 보면 어떨까?
리스트 6의 방법은 앞의 단순 정렬법과는 달리 일단 정렬되지 않는 값들 중에 가장 큰 값이 있는 위치를 알아낸 후 한 번의 교환에 의해 그 값이 정렬되지 않는 값의 맨 뒤로 옮겨지게 된다.
이 방법은 자료의 교환 횟수를 앞의 방법보다 상당히 감소시킨다.
따라서 교환해야 할 자료의 크기가 클수록 효과는 비례해서 증가하게 된다.
(리스트 6) 선택 정렬법을 사용한 예
{
int loop1, loop2;
int temp;
int max_item;
for (loop1 = 0; loop1 < last_item; loop1++)
{
max_item = 0;
for (loop2 = 0; loop2 < (last_item-loop1); loop2++)
{
if (a[max_item] < a[loop2 + 1])
max_item = loop2 + 1;
temp = a[max_item];
a[max_item] = a[max_item – loop1];
a[last_item – loop1] = temp;
}
}
}
(3) 삽입 정렬법(Insertion Sorting)
삽입 정렬 방법도 n개의 킷값에 대하여 n-1단계로 나누어져 수행된다.
버블 정렬과 다른 점은 i번째 단계에서는 앞에서부터 i개의 키가 이미 정렬되어 있으며 i+1번째 위치에 있는 키를 삽입키로 하여 삽입키 앞에 있는 키들과 비교를 수행한다는 것이다.
이 과정에서 i+1번째있는 삽입키는 자신보다 작은 키값을 발견할 때까지 앞에 있는 키들을 차례로 비교하여 자신보다 큰 키들을 뒤로 이동시킨다.
그러면 다음과 같은 예를 생각해 보자.
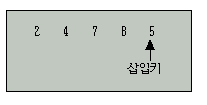
위에서 삽입키 5앞에 있는 4개의 키를 포함하는 리스트는 이미 정렬되어 있으며 키값 5는 8과 비교하여 8이 크므로 8을 뒤로 이동하고, 다음으로 7과 비교하여 7이 크므로 7을 뒤로 이동한다.
다음에 4와 비교할 때 4가 5보다 작으므로 비교하는 것을 멈추고 4다음 위치에 5를 두면, 2, 4, 5, 7, 8의 5개의 키값을 갖는 리스트가 정렬된다.
따라서 삽입 정렬에서 이러한 단계를 n-1번 반복하면 전체 리스트의 정렬이 완료된다.
삽입 정렬에서 삽입키가 정렬된 리스트의 첫 원소보다 더 작은 경우에는 리스트의 범위 밖의 원소와 비교를 시도할 수 있으므로 이를 방지하기 위하여 프로그램 작성시 항상 비교되는 키가 리스트의 첫 원소인가를 확인하는 루틴을 포함시켜야 한다.
이러한 비교를 수행하는 대신 리스트의 맨 앞에 아주 작은 값 -oo(무한대;이하 같음)름 먼저 저장하고 삽입 정렬을 수행하면 이러한 비교에 따른 시간 지체를 줄일 수 있다.
보조 공간에 -oo를 먼저 저장한 후 정렬을 수행하는 예는 그림 5와 같이 나타낼 수 있다.

이러한 과정을 C 프로그램으로 나타내면 리스트 8과 같다.
(리스트 8) 삽입 정렬
void Insertion(int n)
{
int i, j, r;
key[0] = -MAXINT;
for (i = 2; i <= n; i++)
{
j = i – 1;
r = key[i];
while (r < key[j])
{
key[j + 1] = key[j];
j = j – 1;
}
key[j + 1] = r;
}
}
* 삽입 정렬의 분석(이부분이 잘 이해되지 않으시는 분은 “[기초] 알고리즘 수행시간<참고>”강좌를 읽어 보세요).
리스트 8의 Insertion에서 최악의 경우는 매단계에서 삽입하려는 키값과 앞에 정렬된 리스트의 모든 키값들을 비교해야 할 때이며 다음과 같이 키값이 역순으로 입력된 경우가 최악의 경우에 해당한다.
282614119
따라서 최악의 경우, 연산 시간은 다음의 계산에 의하여 O(n2(제곱))으로 표시된다.
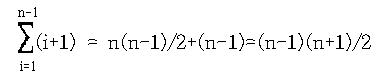
(4) 퀵 정렬법(Quick Sorting)
퀵 정렬의 기본 동작은 정렬하고자 하는 리스트에서 기준이 되는 키를 선정하여 기준키를 적당한 위치로 이동하는 것이다.
이때 리스트에서 기준키를 경계로 기준키보다 앞에 있는 키들은 모두 기준키보다 작거나 같으며 기준키보다 뒤에 있는 키들은 모두 기준키보다 크거나 같게 만든다.
다음과 같은 키들로 구성된 리스트를 생각해 보자.
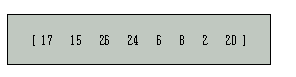
리스트의 첫 원소를 기준키로 선정한 후 다음과 같은 동작을 수행한다.
기준키 바로 다음의 위치부터 뒤쪽으로 기준키보다 큰 키를 찾으며, 동시에 리스트의 마지막 키부터 앞쪽으로 지준키보다 작은 키를 찾아 서로 교환한다.
위의 예에서 기준키는 17로 잡게 되며, 기준키보다 큰 키는 26이 되고 기준키보다작은 키는 2가 되어 서로 교환을 하면 다음과 같은 리스트가 된다.
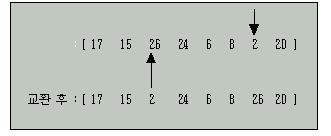
계속해서 다음 키부터 이러한 동작을 반복하면 기준키 17보다 큰 키는 24가 되고 작은 키는 8이 되어 서로 교환하면 다음과 같은 리스트가 된다.
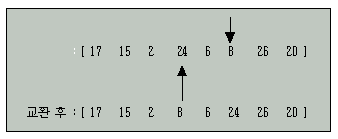
이러한 동작을 계속하면 기준키 17보다 큰 키는 24가 되고 작은 키는 6이 되는 위치를 찾게 된다.
그러나 이번에는 아래의 리스트와 같이 앞쪽에서부터 큰 키를 찾은 위치와 뒤쪽에서부터 작은 키를 찾은 위치가 서로 교차했음을 알 수 있다.
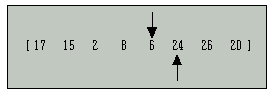
이 경우, 두 키값을 교환하지 않으며 그대신 기준키와 작은 키를 서로 교환하여 다음과 같은 리스트를 만든다.

위의 리스트에서 지준키 17을 경계로 앞쪽 키들은 모두 기준키보다 작으며 뒤쪽 키들은 모두 17보다 큰 것을 알 수 있다.
따라서 기준키 17은 전체 리스트가 정렬이 된 후에도 위치 변동이 없게 된다.
위에서 설명된 기본 동작은 기준키를 제 위치에 놓은 후 원래의 리스트를 앞쪽 키들로 구성된 리스트와 뒤쪽 키들로 구성된 리스트로 양분하므로 이를 분할(Partition)이라 부른다.
먼저 전체 리스트를 분할하여 2개의 리스트로 만들고 분할된 2개의 리스트에 각각 다시 분할을 적용한다.
이러한 반복된 분할을 적용할 때 편의상 왼쪽 리스트를 먼저 분할한다.
앞에서 사용된 예에 대하여 분할을 반복 수행하여 전체 리스트의 정렬을 완로하는 퀵 정렬법의 예는 그림 6에 주어진다.
그림 6에서 m과 n은 분할을 수행할 리스트의 범위를 나타낸다.
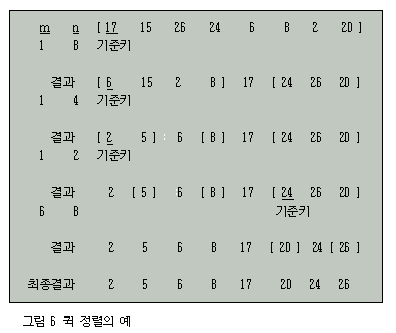
일반적으로 기준키는 항상 분할하고자 하는 리스트의 첫 번째 키로 선정되는데 이러한 선정 방법을 사용하여 퀵 정렬을 C 프로그램으로 작성하면 프로그램 7-4와 같다.
그러나 리스트의 다른 키를 기준키로 선정하는 프로그램을 작성하려면 선정된 키와 리스트의 첫 번째 키를 먼저 교환 후 리스트 9를 이용하면 가능하다.
(리스트 9) 퀵 정렬
void Quick_Sort(int m, int n) // m과 n은 적용범위의 시작과 끝 위치
{
int i, j, k, temp;
if (m < n)
{
i = m;
j = n + 1;
k = key[m]; // 기준키
do { // 분할을 수행하는 do…while 문
do { // 앞에서부터 기준키보다 큰 키 찾기
i = i + 1;
} while (record[i] < k);
do { // 뒤에서부터 기준키보다 작은 키 찾기
j = j – 1;
} while (record[j] > k);
if (i < j)
{ // 큰 키와 작은 키의 교환
temp = key[j];
key[j] = key[i];
key[i] = temp;
}
} while (i <= j);
temp = key[j]; // 기준키와 작은 키의 교환
key[j] = key[m];
key[m] = temp;
Quick_Sort(m, j – 1); // 앞쪽 리스트에 대한 분할을 계속
Quick_Sort(j + 1, n); // 뒤쪽 리스트에 대한 분할을 계속
}
}
* 퀵 정렬의 분석
리스트 9의 Quick_Sort에서 최악의 경우는 매분할이 수행된 후 남은 킷값들이 모두 한쪽의 리스트에 포함되는 것이다.
예를 들면 아래와 같이 이미 정렬된 리스트가 입력될 때 최악의 경우에 해당한다.
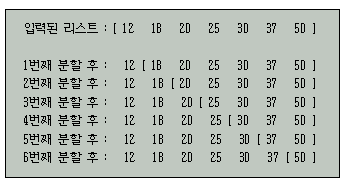
따라서 n개의 키를 갖는 리스트에 대하여 최악의 경우 적용되는 분할의 횟수는 n-1번이며 매분할에 사용되는 비교의 횟수는 적용되는 리스트에 포함된 키들의 수에 비례한다.
그러므로 총 소요 시간은 n+(n-1)+……..+2에 비례하게 되며 O(n2(제곱인거 아시죠?))으로 표시된다.
최악의 경우와는 반대로 최선의 경우는 매분할이 수행된 후 2개의 리스트가 같은 크기로 항상 나누어 지는 것으로 소요시간은 O(nlog2n)이며 평균 소요 시간도 역시 O(nlog2n)이라고 알려져 있다.
(5) 히프 정렬법 (Heap Sorting)
먼저 히프 정렬을 이해하기 위하여 히프라는 자료구조를 정의한다.
이진 트리를 기억공간에 저장할 때 일차원 배열을 사용한다. 일차원 배열의 i번째 위치한 노드의 부모 위치는 ![]() 이고 왼쪽 자식 노드가 있다면 2*i 위치에 있으며 오른쪽 자식 노드가 있다면 2*i+1의 위치에 존재한다(
이고 왼쪽 자식 노드가 있다면 2*i 위치에 있으며 오른쪽 자식 노드가 있다면 2*i+1의 위치에 존재한다( ![]() 는 i/2의 결과에서 소수점 이하의 자리수를 버림).
는 i/2의 결과에서 소수점 이하의 자리수를 버림).
역으로 일차원 배열에 저장된 키값은 이러한 위치 공식에 의하여 이진 트리로 간주될 수 있다.
히프는 다음의 성질을 만족하는 이진 트리이다.
- 1. 히프는 완전 이진 트리이다.
- 2. 루트의 키값은 부분 트리의 노드의 키값보다 크거나 같다.
- 3. 왼쪽 부분 트리와 오른쪽 부분 트리 역시 위 2의 성질을 만족한다.
그림 7은 위의 성질을 만족하는 히프와 일차원 배열에 이러한 히프를 저장한 예를 보여준다.
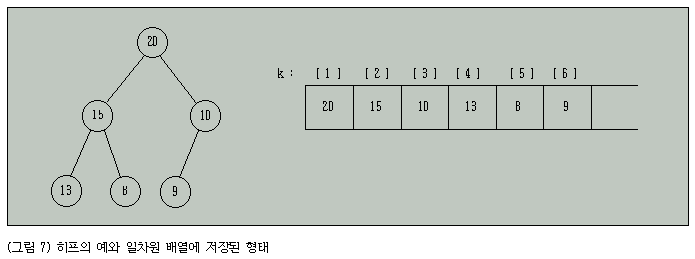
노드를 저장하는 위치를 사용하여 히프의 성질 2를 다시 정의하면 K[i]>=K[2*i] (단 2*i<=n)이고 K[i]>=K[2*i+1] (단 2*i+1<=n)으로 나타낼 수 있다.
그림 7에서 이러한 성질이 만족됨을 알수 있다(이 정의는 최대 히프(max heap)를 나타내며 부등호가 반대 방향이고 최소 히프(min heap)를 나타낸다).
히프 정렬은 두 단계로 나누어 실행되는데 먼저 정렬하고자 하는 리스트를 히프 구조로 만들고 히프 구조에서 정렬을 수행한다.
adjust는 어느 한 노드 x에서 x를 루트로 하는 트리에서 이미 히프이 성질을 만족하는 오른쪽 부분 트리와 왼쪽 부분 트리를 조정하여 x를 포함하는 트리 전체가 히프가 되도록하는 알고리즘이다.
예를 들면 그림 8과 같은 트리를 살펴보자.
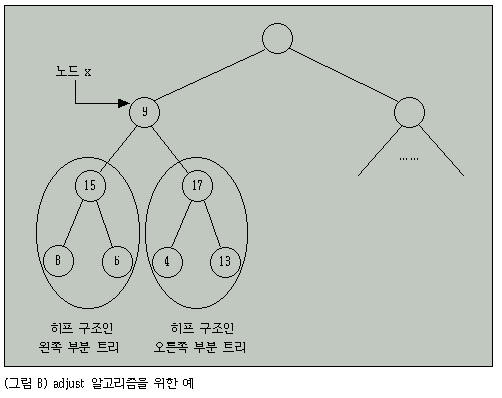
그림 8에서 x로 표시된 노드를 루트로 하는 부분 트리는 현재 히프 구조가 아니나 그 노드의 왼쪽 부분 트리는 각각 히프의 성질을 만족한다.
이때 노드 x를 시작 노드로 하여 왼쪽 자식과 오른쪽 자식을 비교하여 더 큰 노드를 선택, 노드 x와 비교한다.
노드 x가 크면 adjust 알고리즘을 멈추고 노드 x가 작다면 두 노드를 교환하여 교환된 자식 노드에서 이러한 과정을 반복한다.
그림 8의 예에서 과정이 반복되는 것을 보이면 그림 9와 같다.
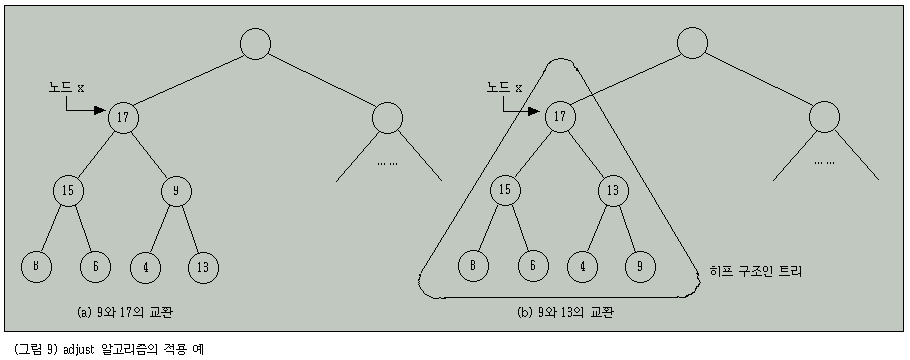
위에서 설명된 adjust 알고리즘을 수행하면 노드 x를 루트로 하는 부분 트리 전체가 히프 구조로 된다.
이때 노드 x의 위치가 i이면 왼쪽 자식의 위치는 2*i이고 오른쪽 자식의 위치는 2*i+1임에 유의하여 adjust 알고리즘을 작성하면 리스트 10과 같다.
(리스트 10) adjust 알고리즘
{
int j, k, done;
done = FALSE;
k = a[i];
j = 2 * i;
while ((j <= n) && (!done)) // 자식노드가 있고 not done일 때까지 반복
{
if (j < n) // 오른쪽 자식노드가 존재하는가?
if (a[j] < a[j + 1]) // 자식노드들 중 큰 노드를 선택
j = j + 1;
if (k >= a[j])
done = TRUE; // 자식노드보다 크므로 반복을 중단
else
{
a[j / 2] = a[j]; // 자식노드와 교환
j = 2 * j;
}
}
a[j / 2] = k;
}
리스트 10에서 adjust 알고리즘은 최악의 경우 시작 노드에서 가장 하위의 노드까지 비교해야 하므로 n개의 노드를 갖는 완전 이진 트리에서는 O(log2n)시간을 필요로 한다.
히프 정렬의 첫 단계는 정렬하고자 하는 리스트를 히프 구조로 만드는 것으로 전체 노드의 수가 n개일 때 ![]() 의 위치에서 시작하여
의 위치에서 시작하여 ![]() -1,
-1, ![]() -2,……,1의 위치에 있는 노드를 시작 노드로 adjust 알고리즘을 반복 수행한다.
-2,……,1의 위치에 있는 노드를 시작 노드로 adjust 알고리즘을 반복 수행한다.
![]() 의 위치에서 시작하는 이유는
의 위치에서 시작하는 이유는 ![]() +1,
+1, ![]() +2,……,n위치에 있는 노드들은 모두 단말 노드이므로 이미 히프 구조를 가지기 때문이다.
+2,……,n위치에 있는 노드들은 모두 단말 노드이므로 이미 히프 구조를 가지기 때문이다.
그림 10은 정렬하고자 하는 키값들을 초기 히프 구조로 만드는 과정을 보여준다.
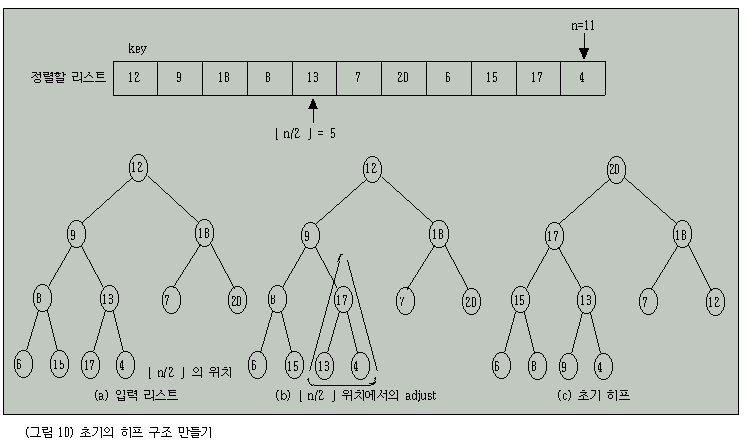
그림 10 (b)는 n/2 번째, 즉 5번째 노드에서 adjust를 수행한 결과를 나타내며, 노드 4, 3, 2, 1에서 차례로 adjust가 수행되었을 때 그림 10 (c)로 되어 전체 리스트가 히프 구조로 되었음을 알 수 있다.
두 번째 단계에서는 히프 구조에서 정렬을 수행하는 것으로 다음의 과정을 반복한다. 전체 트리의 루트를 마지막 노드와, 즉 key[1]과 key[n]을 교환한 후 루트로부터 n-1개의 노드에 대하여 adjust 알고리즘을 수행한다.
방금 교환된 key[n]에 있는 노드는 adjust에서 제외됨에 유의하라.
그림 11은 그러한 과정을 보여준다.
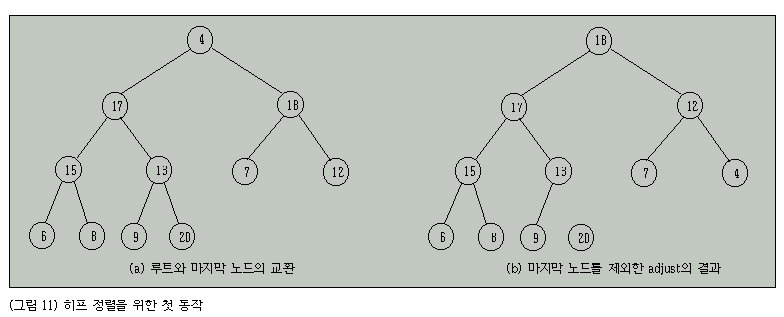
이러한 조정이 끝나면 key[1]과 key[n-1]을 교환한 후 크기를 n-2로 하여 adjust 알고리즘을 다시 수해한다.
이러한 과정을 n-1번 수행하면 리스트의 마지막에서부터 차례로 교환된 키값들이 정렬된 상태로 남게 된다.
그림 12는 최종 정렬이 완료되었을 때의 일차원 배열에 저장된 키들을 보여준다.
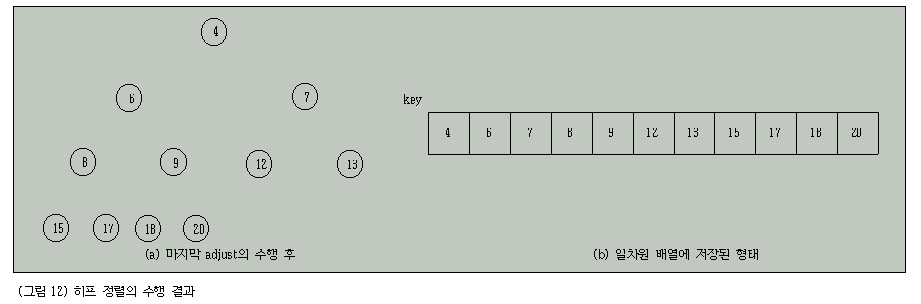
이러한 과정을 C 프로그램으로 작성하면 리스트 11과 같다.
(리스트 11) 히프 정렬
{
int i, temp;
for (i = (n / 2); i >= 1; –i) // 초기 히프 만들기
adjust(key, i, n);
for (i = (n – 1); i >= 1; –i) // 히프 정렬의 두 번째 단계
{
temp = key[i + 1]; // i개의 키에 대하여 adjust 적용
key[i + 1] = key[1];
key[1] = temp;
adjust(key, 1, I);
}
}
* 히프 정렬의 분석
리스트 11에서 첫 번째 for문은 정렬할 리스트를 초기 히프 구조로 만드는 부분이며 O(n)시간이 걸린다고 알려져 있다.
그리고 두 번째 for문은 히프 정렬의 두 번째 단계를 위한 것으로 총 n-1번의 교환과 adjust 알고리즘을 수행하므로 한 번의 adjust 알고리즘이 최악의 경우 O(log2n)시간이 소요되어 총 O(nlog2n)시간이 걸림을 알 수 있다.
따라서 히프 정렬을 위한 시간은 O(nlog2n)이 된다.
(6) 합병 정렬법(Merge Sorting)
일반적으로 합병(merge)이란 각각 정렬된 리스트들을 하나의 정렬된 리스트로 만드는 것이다.
특히 2개의리스트를 합병하는 것을 2원 합병(two way merge)이라 하며 합병의 예를 그림으로 나타내면 그림 13과 같다.
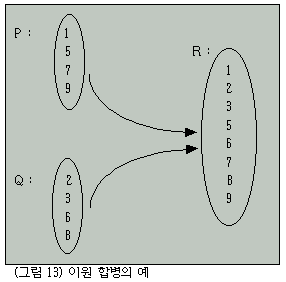
합병 정렬에서는 합병하고자 하는 2개의 리스트가 배열에 존재한다.
두 리스트는 각각 시작 위치와 끝 위치에 의하여 구별된다.
그림 13의 2개의 리스트는 그림 14와 같이 저장된다.
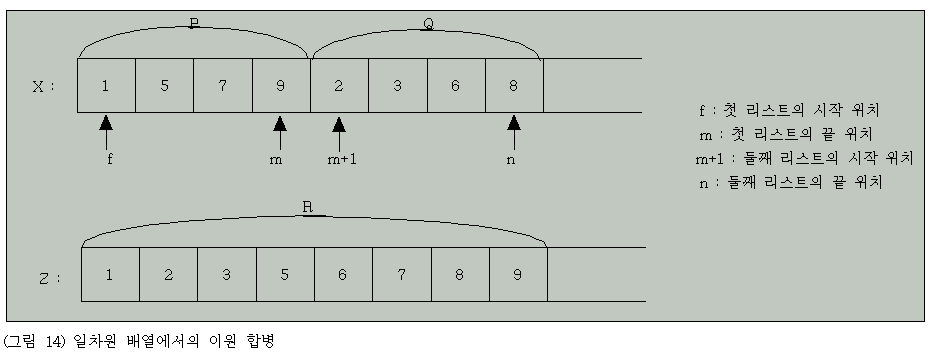
그림 14에서 합병하고자 하는 2개의 리스트는 일차원 배열 X에 저장되어 서로 인접하며 위치를 나타내기 위하여 변수들 f, m, n을 사용한다.
합병된 결과는 같은 크기의 일차원 배열Z에 저장된다.
이러한 합병 과정을 프로그램으로 작성하면 리스트 12와 같다.
(리스트 12) 이원 합병
{
int i, j, k, t;
i = f; // 첫 리스트의 시작 위치
j = m + 1; // 둘째 리스트의 시작 위치
k = f; // 합병 결과를 저장할 리스트의 시작 위치
while ((i <= m) && (j <= n)) // 두 리스트중 하나가 끝날 때까지 반복
{
if (x[i] <= x[j])
{
z[k] = x[i]; // 첫 리스트의 키값을 이동
i = i + 1;
}
else
{
z[k] = x[j]; // 둘째 리스트의 키값을 이동
j = j + 1;
}
k = k + 1;
}
if (i > m)
for (t = j; t <= n; t++) // 둘째 리스트에서 남은 키값을 이동
z[k + t – j] = x[t];
else
for (t = i; t <= m; t++) // 첫 리스트에서 남은 키값을 이동
z[k + t- i] = x[t];
}
리스트 12의 Merge 알고리즘의 시간을 분석하면 while 루프는 두 리스트 중 어느 하나의 리스트의 마지막 키값이 Z로 이동했을 때 끝난다.
그리고 두 리스트 중 어느 한 리스트에 남은 키들이 for문에 의하여 Z로 이동되므로 총 시간은 두 리스트의 키값들의 수에 의하여 결정된다.
따라서 O(n-f+1)의 시간이 소요된다.
합병 정렬에서는 위에서 설명된 합병 알고리즘을 반복해서 사용한다.
먼저 합병될 리스트의 길이(즉 리스트에 포함된 키들의 수)를 1로 하고 두 리스트를 쌍으로 합병을 수행하여 길이가 2인 n/2개의 리스트를 만든다.
계속하여 길이 2인 두 리스트를 쌍으로 하여 길이 4인 리스트로 합병한다.
이 합병 과정은 길이가 n인 하나의 리스트로 합병될 때까지 반복한다.
이 과정을 예로 들면 그림 15와 같다.
그림 15에서 합병된 리스트를 쉽게 구별하기 위하여 대괄호([ ])를 사용한다.
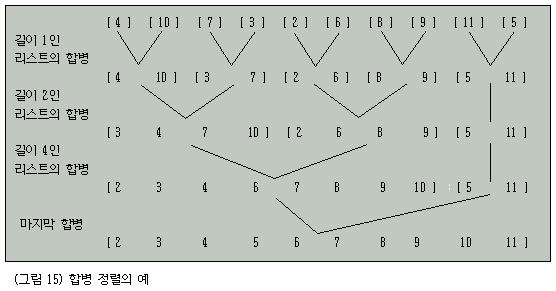
그림 15에서 합병할 리스트를 쌍으로 묶을 때 마지막 남은 리스트의 짝이 없을 때는 그 리스트를 그래로 남겨둔다.
합병 정렬의 알고리즘을 작성하기 전에 그림 15에서와 같이 전체 합병 정렬은 합병할 리스트의 길이에 따라 몇 단계로 나누어져 있음을 알 수 있다.
한 단계에서 합병할 리스트의 쌍들은 모두 같은 길이이며 인접해 있다.
단 마지막 쌍은 서로 다른 길이 일 수 있다.
따라서 각 단계를 프로그램으로 작성할 때 해당 단계에서 적용되는 길이를 매개 변수로 받아들여 두 리스트의 시작 위치와 끝 위치를 결정할 수 있다.
예를 들면, 길이 1인 리스트를 합병할 때 합병할 쌍들의 위치 변수들 (f, m, n)은 (1, 2, 3), (3, 3, 4), (5, 5, 6)……의 순으로 결정된다.
따라서 합병할 리스트의 길이를 매개 변수 length에 받아들일 때, i=1의 초기값에 대하여 (i, i+length-1, i+2*length-1)로 결정되며 매번 i=i+2*length로 증가시킨다.
길이가 2일 때도 이러한 공식이 적용될 수 있음을 알 수 있다.
따라서 이러한 방법으로 length를 매개 변수로 받아들여 한 단계를 수행하는 프로그램을 작성하면 리스트 13과 같다.
(리스트 13) 합병 정렬의 한 단계
{
int i, t;
i = 1;
while (i <= (n – 2 * length + 1)) // 길이가 length인 인접한 두 리스트를 계속해서 합병
{
Merge(x, y, i, i + length – 1, i + 2 * length – 1);
i = i + 2 * length;
}
if ((i + length – 1) < n)
Merge(x, y, i, i + length – 1, n); // 남은 두 리스트를 합병
else
{
for (t = i; t <= n; t++) // 남은 하나의 리스트의 키값들은 그대로 이동
y[t] = x[t];
}
}
리스트 13의 Merge_Pass는 합병하고자 하는 리스트 X의 키들을 합병한 후, 모두 리스트 Z에 저장하므로 연산 시간은 O(n)이 된다.
이제 각 단계에서 합병할 리스트의 길이를 결정하여 리스트 13을 반복시키는 부분을 작성하면 합병 정렬이 되고 리스트 14와 같이 작성할 수 있다.
(리스트 14) 합병 정렬
{
int length;
int y[SIZE];
length = 1; // 리스트의 길이를 1로 초기화
while (length < n) // 합병된 리스트의 길이가 n이 될 때까지 반복
{
Merge_Pass(x, y, n, length); // x에 저장된 리스트를 y에 합병
length = 2 * length; // 리스트의 길이를 두배로 만든다
Merge_Pass(y, x, n, length); // y에 자장된 리스트를 x에 합병
length = 2 * length; // 리스트의 길이를 두배로 만든다
}
}
* 합병 정렬의 분석
리스트 14는 리스트의 길이가 매번 2배씩 증가하므로 반복 횟수는 log2n이며 합병한 리스트의 길이가 n이 되면 정렬이 완료된다.
따라서 리스트 14는 log2n번 리스트 13을 반복 수행하고 리스트 13은 O(n)번의 시간을 소요하므로 총 소요 시간은 O(nlog2n)이 된다.
* 알고리즘의 수행시간 분석 *
* 프로그램의 성능 분석
프로그램은 주어진 작업의 수행을 위하여 올바른 알고리즘의 구조적 구현이 필요하며, 이에 따른 다음과 같은 평가가 필요하다.
- 1. 주어진 작업을 의도한 대로 바르게 수행하는가?
- 2. 프로그램은 모듈화되어 있으며, 읽거나 이해하기 쉽고, 수정하기 쉬우며, 설명이 잘 되어 있는가?
프로그램의 수행 성능을 객관적으로 비교하기 위해서는 이를 위한 기준 척도가 있어야 하는데, 다음의 두 가지 측면을 고려할 수 있다.
- 1. 수행시간 : 프로그램이 의도된 작업의 처리를 시작하여 이를 완료하기까지의 수행에 소요된 시간으로, 수행 시간이 짧을수록 성능은 우수하다고 평가한다.
이는 프로그램을 구상하고, 작성하고, 수정 및 번역하는 등의 프로그램 개발의 성능이 아닌 수행상의 성능, 즉 프로그램이 의도한 작업을 얼마나 빨리 수행하는냐의 평가이다. - 2. 자원의 점유 : 프로그램의 수행을 위해 필요한 자원(메모리 등)의 양으로, 점유되는 자원의 양은 작을수록 성능이 우수하다고 평가한다.
특히 멀티프로그래밍의 경우에는 여러 프로그램들이 자원들을 공유하므로 이 항목이 매우 중요하다.
이 항목 중에서 프로세서의 점유량은 앞의 수행 시간에 의해 반영되므로, 자원의 점유는 주로 사용되는 주메모리의 용량에 의해 평가된다.
실제로 이 두 가지 항목은 서로 이율배반적일 수 있다.
즉, 메모리를 많이 사용하여 수행 시간을 짧도록 할 수도 있으며, 그 반대로 수행 시간을 늘려서 메모리를 적게 사용할 수도 있다.
그러므로 이 두 가지 항목을 혼합하여 평가하는 것이 바람직하다.
다섯 가지 알고리즘이 제안된 경우, 실제로는 다섯 가지 알고리즘 중 가장 우수한 한 가지 알고리즘만을 사용하려는 의도에서, 단지 성능 비교를 위해 다섯 가지 알고리즘을 모두 구현하여 수해시켜 보는 것은 매우 비효율적인 방법이다.
알고리즘을 프로그램으로 구현하고 실제 컴퓨터에서 수행하지 않고도, 그 알고리즘의 수행 시간과 요구되는 자원의 양을 예측할 수는 없을까?
그 방법이 바로 모델링이다.
모델링은 실제 상황과 근사한 임의의 상황을 설정하고 그로부터 필요한 자료를 예측해내는 과정이다.
이제 모델링을 이용하여 알고리즘의 성능을 예측하기 위해, 수행 시간의 분석 방법을 소개한다.
* 수행 시간의 분석
실제 프로그램의 수행 시간은 알고리즘(프로그램)의 구조뿐 아니라 프로그램에 대한 입력과 수행 컴퓨터의 상태(사용자수, 메모리 용량 등)에 의해 영향을 많이 받는다.
그리하여 알고리즘(실제로는 이를 구현한 프로그램)의 수행을 통한 정확한 시간의 측정은 그 투자 시간 및 노력에 비해 분석 결과의 효율성은 크지 못하다.
그러므로 본 분석에서는 필요한 정확성을 유지하며 손쉽게 구할 수 있는 근사적 분석법을 설명하고 이를 활용하도록 하겠다(지금부터 수학이..^^).
실수에 대해 정의된 실함수 f, g가 있다고 하자. 프로그램의 수행시간을 실함수로 나타내는 방법은 뒤에서 다룬다.
N과 같거나 큰 모든 n(n>=N)에 대해 f(n)=
물론 f(n)=
예를 들어, 어떤 프로그램의 수행시간을 T(n)이라 하자.
여기서 n은 그 프로그램에 대한 입력의 크기를 의미한다.
수행시간 T(n)은 실제 프로그램이 수행되는 컴퓨터에 따라 큰 영향을 받으므로, 초와 같은 시간 단위가 아닌 수행되는 명령어의 수로 표시하는 경우가 많다.
이 경우에 컴파일러 등에 의한 영향을 고려하여 수행시간은 절대적 수치가 아닌 n에 비례한다는 표현을 사용한다.
크기가 n인 모든 입력에 대한 프로그램의 수행 시간은 항상 같지 않으므로 T(n)의 최소값, 평균값, 최대값을 생각할 수 있는데, 이중 평균값은 실제 비교시 의미가 적고 계산하기도 매우 어려우므로 최대값을 비교한다.
크기가 n인 모든 입력에 대한 수행 시간의 최대치(Worst Case)를 cn2(제곱^^)이라 하면 T(n)=
즉 어떤 상황에서도, 이 프로그램의 수행시간(T(n))은 수행에 필요한 입력 개수의 제곱(n2)의 상수배 이하가 됨을 알 수 있다.
실제 프로그램의 수행시간을 상수항으로 표시하는 것은 매우 어려우나, 프로그램을 여러 단계로 나누고 각 단계에 대한 수행 시간을 빅오로 정하고, 전체 수행시간은 각 단계별 수행 시간에 대해 빅오의 연산을 이용하면 가능해진다.
빅오의 대표적 연산이 덧셈과 곱셈은 다음과 같이 수행된다.
n개의 입력을 갖는 2개 프로그램의 수행시간을 각각 T1(n)과 T2(n)이라 하고, 이들은 또한 각각 T1(n)=O(f)=
예를 들어 T1(n)=
T1(n)+T2(n)=O(max(n3,n2))=O(n3)=
이 된다.
빅오의 곱셈의 법칙은 n개의 입력을 갖는 2개 프로그램의 수행시간을 앞에서와 같이 각각 T1(n)과 T2(n)이라 할 때, T1(n)*T2(n)=O(f(n)*g(n))이 된다.
실제 프로그램의 수행시간을 분석하는 방법은, 먼저 프로그램의 각 문장에 대한 수행시간을 빅오로 표현한 후, 문장 수행 구조에 따라 앞의 덧셈과 곱셈의 법칙들을 사용하여 전체 프로그램의 수행시간을 분석할 수 있다.
C언어의 대표적인 문장의 수행시간의 분석은 다음과 같다.
- 1. 치환문, 입출력문 등의 수행시간은 상수항이므로 O(1)로 표현한다.
- 2. 수차적 제어 구조에 의한 문장들은 앞에서 제시한 덧셈의 법칙에 의해 수행시간을 정한다. 따라서 순차적으로 수행되는 제어 구조의 경우에는 최대 수행시간을 갖는 문장의 수행시간을 빅오로 표현하면 된다.
- 3. 조건적 제어 구조인 if then else문에서는 조건을 조사하는 시간과 조건에 따라(참 또는 거짓) 수행되는 부분의 수행시간에 덧셈의 법칙을 적용한다. switch문에서는 조건을 조사하는 시간과 조건의 계산에 따라 수행되는 case문의 수행 시간의 합이 된다.
- 4. 반복적 제어 구조인 for문장에서는 반복 조건 조사와 반복 자료 처리 시간의 합과 반복 횟수와 곱이며, while 및 애 while 문장의 경우에는 조건 조사 및 반복 수행시간의 합이 된다. 이때 이 시간은 반복되는 횟수만큼 곱해지며, 반복이 끝나는 조건에서는 반복 조건 시간만이 더해진다. 특히 반복문이 중첩된 경우에는 반복 횟수의 계산에 유의해야 한다.
이제 다음의 실제 프로그램에 대해 전체 수행 시간을 구해 보자.
(리스트 7) 수행 시간을 분석할 프로그램
#include <stdio.h>
#define N 7
main()
{
(1)int cnt = 0, i, j, k;
(2)for (i = 0; i <= N; ++i)
(3)for (j = 0; j <= N; ++j)
(4)for (k = 0; k <= N; ++k)
(5)if (i + j + k == N) {
(6)++cnt;
(7)printf(“%3d%3d%3d\n”, i, j, k);
(8)}
(9)printf(“count is : %d\n”, cnt);
}
리스트 7은 더하여 7이 되는 세 수를 찾는 프로그램으로, 중첩된 3개의 for 문장 안에 if문이 있다.
선언문 (1)은 수행시간이 필요 없고, 출력문(9)는 수행시간이 O(1)이고 한 번만 수행된다.
반복 수행되는 (2)에서 (8)까지의 수행 시간을 구하여 (9)의 수행 시간과 합하면 전체 수행시간이 된다.
(5)문장에서, if 문장의 조건식 조사에는 O(1)의 시간이 소요된다.
조건이 만족되는(참인) 경우에는 (6) 및 (7) 문장을 수행하며 이의 수행시간은 O(max(1,1))=O(1)이고, 조건이 만족되지 않는 경우에는 수행내용이 없으므로 수행 시간은 0이다.
따라서, 조건이 만족되든 아니든 ifans의 수행시간은 O(1)이 된다.
if 문장이 수행되는 횟수는 (N+1)3(세제곱;for 문장이 세 번 중첩되어 있음)이므로, (2)에서 (8)까지의 수행시간은 곱셈의 법칙에 의해 O(N3(세제곱)*1)=O(N3)이 된다.
전체 main 함수의 수행시간은 덧셈의 법칙에 의해 O(N3+1)=O(N3)이 된다.